【乐虎集团的官方网站
】利用滚动轴承振动信号分析故障诊断的方法可分为简易诊断法和精密诊断法两种。简易诊断的目的是为了初步判断被列为诊断对象的滚动轴承是否出现了故障;精密诊断的目的是要判断在简易诊断中被认为出现了故障的轴承的故障类别及原因。下面介绍了5种常见的简易诊断方法:
1. 振幅值诊断法
这里所说的振幅值指峰值Xp、均值X(对于简谐振动为半个周期内的平均值,对于轴承冲击振动为经绝对值处理后的平均值)以及均方根值(有效值)Xrms。这是一种z*简单、z*常用的诊断法,它是通过将实测的振幅值与判定标准中给定的值进行比较来诊断的。
峰值反映的是某时刻振幅的z*大值,因而它适用于像表面点蚀损伤之类的具有瞬时冲击的故障诊断。另外,对于转速较低的情况(如300r/min以下),也常采用峰值进行诊断。
均值用于诊断的效果与峰值基本一样,其优点是检测值较峰值稳定,但一般用于转速较高的情况(如300r/min以上)。
均方根值是对时间平均的,因而它适用于像磨损之类的振幅值随时间缓慢变化的故障诊断。
2. 波形因数诊断法
波形因数定义为峰值与均值之比(Xp/X)。该值也是用于滚动轴承简易诊断的有效指标之一。如图1所示,当Xp/X值过大时,表明滚动轴承可能有点蚀;而Xp/X小时,则有可能发生了磨损。
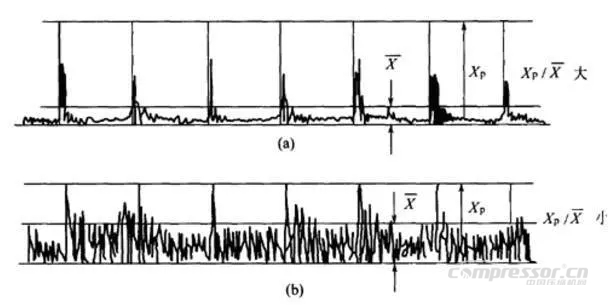 图1 滚动轴承冲击振动的波形因数
3. 波峰因数诊断法
波峰因数定义为峰值与均方根值之比(XP/Xrms)。该值用于滚动轴承简易诊断的优点在于它不受轴承尺寸、转速及载荷的影响,也不受传感器、放大器等一、二次仪表灵敏度变化的影响。该值适用于点蚀类故障的诊断。通过对XP/Xrms值随时间变化趋势的监测,可以有效地对滚动轴承故障进行早期预报,并能反映故障的发展变化趋势。当滚动轴承无故障时,XP/Xrms为一较小的稳定值;一旦轴承出现了损伤,则会产生冲击信号,振动峰值明显增大,但此时均方根值尚无明显的增大,故XP/Xrms增大;当故障不断扩展,峰值逐步达到极限值后,均方根值则开始增大,XP/Xrms逐步减小,直至恢复到无故障时的大小。
4. 概率密度诊断法
无故障滚动轴承振幅的概率密度曲线是典型的正态分布曲线;而一旦出现故障,则概率密度曲线可能出现偏斜或分散的现象,如
图1 滚动轴承冲击振动的波形因数
3. 波峰因数诊断法
波峰因数定义为峰值与均方根值之比(XP/Xrms)。该值用于滚动轴承简易诊断的优点在于它不受轴承尺寸、转速及载荷的影响,也不受传感器、放大器等一、二次仪表灵敏度变化的影响。该值适用于点蚀类故障的诊断。通过对XP/Xrms值随时间变化趋势的监测,可以有效地对滚动轴承故障进行早期预报,并能反映故障的发展变化趋势。当滚动轴承无故障时,XP/Xrms为一较小的稳定值;一旦轴承出现了损伤,则会产生冲击信号,振动峰值明显增大,但此时均方根值尚无明显的增大,故XP/Xrms增大;当故障不断扩展,峰值逐步达到极限值后,均方根值则开始增大,XP/Xrms逐步减小,直至恢复到无故障时的大小。
4. 概率密度诊断法
无故障滚动轴承振幅的概率密度曲线是典型的正态分布曲线;而一旦出现故障,则概率密度曲线可能出现偏斜或分散的现象,如
 图2 滚动轴承的损伤
5. 峭度系数诊断法
峭度(Kurtosis)β定义为归一化的4阶中心矩,即:
图2 滚动轴承的损伤
5. 峭度系数诊断法
峭度(Kurtosis)β定义为归一化的4阶中心矩,即:

振幅满足正态分布规律的无故障轴承,其峭度值约为3。随着故障的出现和发展,峭度值具有与波峰因数类似的变化趋势。此方法的优点在于与轴承的转速、尺寸和载荷无关,主要适用于点蚀类故障的诊断。
图3为一轴承疲劳试验的结果。试验中第74h轴承发生了疲劳破坏,峭度系数由3上升到6[图(a)],而此时峰值[图(b)]和RMS值尚无明显增大。故障进一步明显恶化后,峰值、RMS值才有所反映。
图中虚线表示在不同转速(800~2700r/min)和不同载荷(0~11kN)下进行试验时上述各值的变动范围。很明显,峭度系数的变化范围z*小,约为士8%。轴承的工作条件对它的影响z*小,即可靠性及一致性较高。
有统计资料表明,使用峭度系数和RMS值共同来监测,滚动轴承振动情况,故障诊断成功率可达到96%以上。
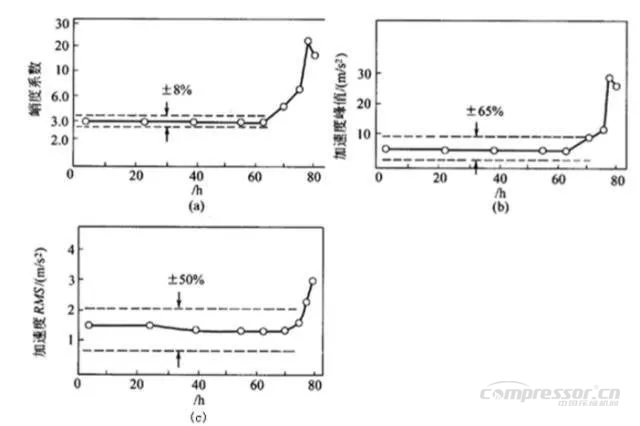 图3 轴承疲劳试验过程
图3 轴承疲劳试验过程
【乐虎集团的官方网站
】利用滚动轴承振动信号分析故障诊断的方法可分为简易诊断法和精密诊断法两种。简易诊断的目的是为了初步判断被列为诊断对象的滚动轴承是否出现了故障;精密诊断的目的是要判断在简易诊断中被认为出现了故障的轴承的故障类别及原因。下面介绍了5种常见的简易诊断方法:
1. 振幅值诊断法
这里所说的振幅值指峰值Xp、均值X(对于简谐振动为半个周期内的平均值,对于轴承冲击振动为经绝对值处理后的平均值)以及均方根值(有效值)Xrms。这是一种z*简单、z*常用的诊断法,它是通过将实测的振幅值与判定标准中给定的值进行比较来诊断的。
峰值反映的是某时刻振幅的z*大值,因而它适用于像表面点蚀损伤之类的具有瞬时冲击的故障诊断。另外,对于转速较低的情况(如300r/min以下),也常采用峰值进行诊断。
均值用于诊断的效果与峰值基本一样,其优点是检测值较峰值稳定,但一般用于转速较高的情况(如300r/min以上)。
均方根值是对时间平均的,因而它适用于像磨损之类的振幅值随时间缓慢变化的故障诊断。
2. 波形因数诊断法
波形因数定义为峰值与均值之比(Xp/X)。该值也是用于滚动轴承简易诊断的有效指标之一。如图1所示,当Xp/X值过大时,表明滚动轴承可能有点蚀;而Xp/X小时,则有可能发生了磨损。

图1 滚动轴承冲击振动的波形因数
3. 波峰因数诊断法
波峰因数定义为峰值与均方根值之比(XP/Xrms)。该值用于滚动轴承简易诊断的优点在于它不受轴承尺寸、转速及载荷的影响,也不受传感器、放大器等一、二次仪表灵敏度变化的影响。该值适用于点蚀类故障的诊断。通过对XP/Xrms值随时间变化趋势的监测,可以有效地对滚动轴承故障进行早期预报,并能反映故障的发展变化趋势。当滚动轴承无故障时,XP/Xrms为一较小的稳定值;一旦轴承出现了损伤,则会产生冲击信号,振动峰值明显增大,但此时均方根值尚无明显的增大,故XP/Xrms增大;当故障不断扩展,峰值逐步达到极限值后,均方根值则开始增大,XP/Xrms逐步减小,直至恢复到无故障时的大小。
4. 概率密度诊断法
无故障滚动轴承振幅的概率密度曲线是典型的正态分布曲线;而一旦出现故障,则概率密度曲线可能出现偏斜或分散的现象,如

图2 滚动轴承的损伤
5. 峭度系数诊断法
峭度(Kurtosis)β定义为归一化的4阶中心矩,即:

振幅满足正态分布规律的无故障轴承,其峭度值约为3。随着故障的出现和发展,峭度值具有与波峰因数类似的变化趋势。此方法的优点在于与轴承的转速、尺寸和载荷无关,主要适用于点蚀类故障的诊断。
图3为一轴承疲劳试验的结果。试验中第74h轴承发生了疲劳破坏,峭度系数由3上升到6[图(a)],而此时峰值[图(b)]和RMS值尚无明显增大。故障进一步明显恶化后,峰值、RMS值才有所反映。
图中虚线表示在不同转速(800~2700r/min)和不同载荷(0~11kN)下进行试验时上述各值的变动范围。很明显,峭度系数的变化范围z*小,约为士8%。轴承的工作条件对它的影响z*小,即可靠性及一致性较高。
有统计资料表明,使用峭度系数和RMS值共同来监测,滚动轴承振动情况,故障诊断成功率可达到96%以上。

图3 轴承疲劳试验过程




网友评论
条评论
最新评论