【乐虎集团的官方网站
】一、序言
W型nianxiangyuan
在工业应用上非常常见,然而它内部的结构绝大多数都是单曲拐结构。能不能将曲轴设计成三曲拐的结构?
记得十多年前在新闻联播中看过沈鼓、陕鼓一些大型nianxiangyuan
三曲拐曲轴加工的画面,当时就想过小型W型无油机能否也采用这种三曲拐的结构?现在的一些nianxiangyuan
教材里没有提及角度式三曲拐W型nianxiangyuan
,仅是详细分析介绍了角度式单曲拐W型60°nianxiangyuan
一些理论。三曲拐的曲轴在一些大型的卧式机器中有应用,课本中对这种结构的机器进行了惯性力的分析。虽然目前教材上没有提及该种结构,但不代表这种结构不能合法存在。只是这种结构在一阶惯性力平衡方面有它的弊端,然而在其它方面也有它的优点。因前期对单曲拐W型各种角度的nianxiangyuan
一、二阶往复惯性力进行了详细分析计算,因而信手拈来将三曲拐的结构也进行详细分析,期望从理论上揭示该种结构的特点,以期扩展nianxiangyuan
的结构,推动国内nianxiangyuan
技术的发展。
本文以关于中心点对称的三曲拐、W型各种角度式nianxiangyuan
为例,考虑到往复质量的差异,从理论上分析推导出机器的一、二阶往复惯性力的公式,分析各种因素对机器的影响,从而遴选出性价比高的结构,可以尝试作为未来的工业应用。该惯性力作用点为曲轴箱体中心点,其大小和变化形成了惯性力的矢端轨迹力图。根据该公式,提出合适的平衡一、二阶往复惯性力的措施。创新拓展nianxiangyuan
理论和结构型式,推动全球范围内W型nianxiangyuan
的升级换代。
二、基础理论
1.正方向的问题
三曲拐W型nianxiangyuan
是指曲轴有三个拐,拐拐之间互成120°且不在同一个运动平面,能够获得旋转惯性力的自动平衡。三个拐所装配的连杆中心距相等,如图1所示。我们这里考虑两级nianxiangyuan
,它有两个一级一个二级,设一级的往复部件质量为ms1,二级往复部件质量为ms2,以图1中间的一列ms2为基准建立直角坐标系xoy,图2与图3中都是以ms2列为基准建立坐标系,这是考虑到有两种质量参与计算的方便。然而对于ms2列偏置分布建立的坐标系不是系统结构的主方向,不容易看出一、二阶惯性力的特征,需要运用到坐标矩阵变换关系式。规定投影到曲柄方向为x轴,与曲柄垂直的方向为y轴。这里规定x轴正方向是由机器中心向外指,这与nianxiangyuan
中将连杆受拉伸规定为正值相吻合,nianxiangyuan
动力计算时也将曲柄在上死点位置时运动部件受到的往复惯性力为正的最大值。y轴的正方向规定为将x轴顺旋转方向转一直角方向为其正方向。这样的规定都是为了方便计算,为后面的各种计算打下基础,也更容易发现规律。
2.研究手段问题
本文采用欧拉公式研究三列惯性力矢量的合力问题,将教科书上推导过程中采用垂直和水平方向两个式子合并成一个式子,这里规定x轴代表向量的实部,y轴代表向量的虚部,二者连接采用虚数单位i来连接。运用到的相关公式如下:

e为工程指数,i为虚数单位,θ为曲柄转角,单位为弧度,规定顺时针旋转方向为正值,θ为变量函数。该式子描述的也就是单位圆。

该式子也是上复数的共轭复数。

一阶惯性力是余弦函数,本文将一对互为共轭的复数的平均值来研究一、二阶惯性力。

它巧妙地运用到两个不同相位的欧拉函数的代数和来研究惯性力的投影问题。式子的右边正好是图1中右边列一阶惯性力投影到xoy坐标系上两个方向上两个力的大小。图1中气缸间夹角γ为60°,由于曲拐间的夹角都是120°,所以右边的活塞工作相位值为 ,根据前面规定了x、y轴的正方向,注意到上式的虚部应为正值。上式子描述的力是相对于中间为基准超前的列的一阶惯性力。大家发现,该式子就是将单曲拐落后的列的力的代数式取其共轭复数来计算。
,根据前面规定了x、y轴的正方向,注意到上式的虚部应为正值。上式子描述的力是相对于中间为基准超前的列的一阶惯性力。大家发现,该式子就是将单曲拐落后的列的力的代数式取其共轭复数来计算。
将该式的“γ”用“-γ”代替后形成新的公式就是图1中左边列的一阶惯性力。




该式子是图1中左边列二阶惯性力投影到xoy坐标系上两个方向上两个力的大小。可以验算当θ为0时,该列的相位角为-60°,所以其二阶惯性力为上式。同样的,将该式的“γ”用“-γ”代替后形成新的公式就是图1中右边列的二阶惯性力的计算公式。
上面两个公式仅对夹角为60°的适用,对其它角度例如45°的要给予修正。
3.研究切入点问题
本文研究惯性力的计算公式及其图像,顾及三列不同的往复质量对计算公式的影响,所以研究的起始点非常重要。文章分析了两种往复质量的计算公式,为计算方便,通常θ角的计入零点规定为ms2列活塞处于上死点的位置。文中得到的计算公式与选择上面的计入零点无关,也就是说,当将自变量θ转换成主方向位置时,只需要将所有公式里作相应的带入变换。
三、计算过程
文中分析了ms2列活塞居中布置和偏置一边时顺时针及反时针旋转时一、二阶往复惯性力的计算公式。考虑到二级nianxiangyuan
有两种往复质量,居中布置与偏置布置结构上有所不同,需要针对各自的型式进行单独研究,得到的惯性力公式形式迥异,所进行的坐标系矩阵变换工作量也不相同,偏置布置需要进行大量的矩阵变换而居中布置无需进行;偏置布置时顺、反时针旋转这两种情况比较起来,得到的惯性力公式基本相同,仅相差几个正负号而已。
三列活塞套入三个曲柄销的先后顺序形成的惯性力矩也各不相同,虽然微小,本文不作研究。文中假设三列都在同一个往复运动平面上往复惯性力合成后的矢端轨迹图像。
1.用基础理论分析图1形式三曲拐顺时针转动时惯性力


r为曲柄半径。ω为旋转角速度,以弧度计入计算。C为后文列出的公式书写方便引入的记号。

1.1一阶惯性力的计算


上式若采用三角函数来运算,则就是下面的两个式子






对(7)式再进行运算化简

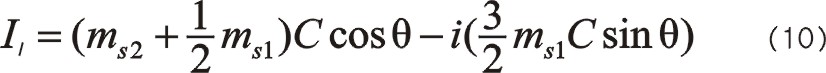
这是居中布置时三曲拐W型夹角60°一阶往复惯性力复数表达式。


当两个质量相等时,即是

一阶力矢在ms2=ms1时成圆的变化,其方向与曲柄转动的方向正好相反,大小与单曲拐的该种型式相同。不能采用在曲柄的反方向加一合适的平衡重来完全平衡掉一阶往复惯性力,需要采用其它合适的机构来平衡一阶惯性力。
若ms2>ms1,则此时的一阶惯性力图是椭圆。由于ms2居中分布时所建立的坐标系属于主方向的位置,其一阶惯性力运动形式与单曲拐的该种结构比较起来,惯性力图形状相同仅转动方向不同,所以它们的长轴都在x轴上,也就是图示中的竖直方向,短轴在水平方向。这种情形不同于偏置分布时的状况。
1.2二阶惯性力的计算


式中λ为曲柄半径连杆比。






这是居中布置时三曲拐W型夹角60°二阶往复惯性力复数表达式。





同样的,若采用三角函数来运算,则是下面的两个式子






二阶力矢在ms2=ms1时成短长轴比为1:3的椭圆变化。这种布置时θ为0°时,力矢到达该椭圆的短半轴位置,曲柄方向矢与二阶力矢在同一方向,但在该瞬时曲柄转向与二阶惯性力变化方向互为反方向。二阶惯性力旋转方向与单曲拐的该种型式不同。
若ms2>ms1,同样的,由于ms2居中分布时所建立的坐标系属于主方向的位置,其二阶惯性力运动形式与单曲拐的该种结构比较起来,惯性力图形状相同仅转动方向不同,所以这种情形时会使原短长轴比为1:3的椭圆有所微量变化。但不会引起椭圆偏转,这与偏置分布时的不同。一、二阶惯性力图因往复质量的不同都不会引起椭圆偏转可以理解为,左右两个ms1共同作用所引起的惯性力的合力导致的。
2.用基础理论分析图2形式三曲拐顺时针转动时惯性力

2.1一阶惯性力的计算





该式用到了三角函数的和差化积公式。




上式表明,一阶惯性力矢端轨迹是一椭圆,变化的周期和曲轴旋转的周期相同。在建立的xoy直角坐标系中,该椭圆的图像是标准的椭圆图像。如果从主方向即x'oy'直角坐标系来看,它不是标准椭圆,相当于将该主方向上的标准椭圆反时针旋转了30°。
若ms2>ms1,长半轴为 ,长轴在ms2列气缸轴线上;短半轴为
,长轴在ms2列气缸轴线上;短半轴为 ,短轴在ms1列气缸轴线上。由于ms2偏置分布时所建立的坐标系不属于主方向的位置,其一阶惯性力运动形式与单曲拐的该种结构比较起来,惯性力图形状相同仅转动方向不同。若ms2=ms1,椭圆退化成圆,半径为
,短轴在ms1列气缸轴线上。由于ms2偏置分布时所建立的坐标系不属于主方向的位置,其一阶惯性力运动形式与单曲拐的该种结构比较起来,惯性力图形状相同仅转动方向不同。若ms2=ms1,椭圆退化成圆,半径为 。
。
2.2二阶惯性力的计算









这是该种偏置布置不向自身旋转时三曲拐W型夹角60°二阶往复惯性力复数表达式。

这是其二阶惯性力参数方程的表达式。
为寻找上方程所描述的图像,先假定两个往复质量相等,利用寻找两个变量的二次多项式方程方法和矩阵转换法来进行。下面仿上面的假设,推导出它是一椭圆的依据。




根据线性代数中二次多项式的判别式定理,满足上两个条件,所以二阶惯性力也是一个椭圆。
由图1可以看出,原坐标系作正值旋转30°后到x'oy'坐标系,也就是将坐标系作逆时针旋转30°,作坐标系的矩阵变换的因子为



上式清晰地表明二阶惯性力的轨迹是椭圆,变化的周期是曲轴旋转周期的一半。经坐标系的旋转变换后的参数方程表明:该椭圆的长半轴是短半轴的3倍,二阶惯性力旋转方向与单曲柺的该种型式不同,曲柄转向与二阶惯性力变化方向互为反方向。不论是在xoy坐标系还是在x'oy'坐标系中,其椭圆的长半轴始终在水平方向,这与三列活塞在旋转平面的分布紧密联系。后文还分析表明,不论ms2处于偏置还是中间位置,不论旋转方向,二阶惯性力矢端力图始终是椭圆,该椭圆的长轴始终处于水平方向,不过其相位变化比较复杂。式(27)可以看出θ为15°时,力矢到达该椭圆的长半轴正的位置,这两个矢量不在同一方向成15°;θ为60°时,力矢到达该椭圆的短半轴负的位置,这两个矢量不在同一方向成120°。二阶惯性力的变化比曲轴自身旋转变化快一倍。
结合图2可得,形如式(25)、(26)参数方程,其图像是将标准直角坐标系中短长轴之比为1:3的椭圆反针旋转30°所得到的图象。
若ms2>ms1,同样的,由于ms2偏置分布时所建立的坐标系不属于主方向的位置,其二阶惯性力运动形式与单曲拐的该种结构比较起来,惯性力图形状相同仅转动方向不同,所以这种情形时会使原短长轴比为1:3的椭圆有所微量变化,并且会引起椭圆偏转。这是由于同一侧两个ms1共同作用所引起的惯性力的合力导致的。ms2列质量越大,原1:3的椭圆长轴越靠近ms2列,亦即长轴向ms2列旋转,这与单曲拐的一样仅二阶惯性力的旋转方向不同。
3.用基础理论分析图3形式三曲拐反时针转动时惯性力

3.1一阶惯性力的计算







该式表明反时针旋转时,一阶惯性力复数方程和直角坐标方程形式上与顺时针旋转时完全相同,说明同是三曲拐W型60°布置时,轨迹力图与转向无关,上述这种布置曲柄矢和一阶惯性力旋转矢也是互为反方向。当二者质量相等时,就成圆的变化,但不能在曲柄的反方向加一合适的平衡重来平衡一阶往复惯性力,需要设计其它的机构来平衡一阶惯性力。
在建立的xoy直角坐标系中,该椭圆的图像是标准的椭圆图像。如果从主方向即x'oy'直角坐标系来看,它不是标准椭圆,相当于将该主方向上的标准椭圆反时针旋转了30°。
3.2二阶惯性力的计算





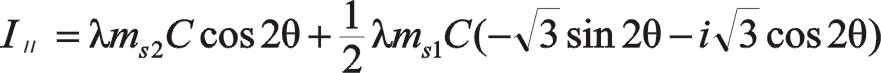


上式表明反时针旋转时,二阶惯性力直角坐标方程形式上与顺时针旋转时不同。说明换一个方向旋转时,需要另一种方程描述二阶惯性力的表现形式,后文的计算表明,它们的轨迹力图是相同的。文章从理论提供了这些状况时力矢的数学表达式,理论上也能够找到一种合适的机构加装上来平衡二阶往复惯性力。




坐标系作负值30°旋转变换到x'oy'坐标系中



结合图3可得,形如式(30)、(31)参数方程,其图像是将标准直角坐标系中短长轴之比为1:3的椭圆顺针旋转30°所得到的图象。
4.一致性验算
由图1、图2、图3,利用坐标系的旋转变换得出其公式的一致性。










也可以由向自身旋转时的代数方程推导出不向自身旋转时的代数方程,而不经过中间列来过渡,即由图3与图2之间的关系,将图3的状况依图示旋转120°后就是图2的状况。其矩阵方程如下





上式二阶方程验算过程的成立是通过下面的矩阵乘法运算得到的:

5.总结
从上面的三种情况分析和计算,可以得出三曲拐W型60°布置有两个ms1,一个ms2往复质量时有以下结论:
5.1一阶惯性力是一椭圆,ms2列中心线是该椭圆的一个对称轴方向,不论ms1、ms1、ms2在运动平面上如何分布,若ms2>ms1,则长轴在ms2列方向,反之则短轴在ms2列方向。
5.2二阶惯性力也是一椭圆,若ms1=ms2,不论采用上面三种情况的特殊情形来计算,该椭圆的长轴始终在水平方向,短轴在竖直方向,并且长半轴是短半轴的3倍。
5.3曲柄矢和一阶、二阶惯性力旋转矢都是互为反方向,这与单曲拐的完全不同而数值相同。
5.4以上讨论的都是关于惯性力对于往复质量ms以及夹角γ对其图像的影响,也讲到了实时的相位对应实时的图像。如果我们从惯性力图像变化率角度来刻画这一理论,就需要用到开普勒定律,这在论文总结中详细论述。
四.举例分析
本文以安徽华晶机械有限公司生产的WW-0.9/10B-Q型单曲拐全无油空压机为例分析该二级nianxiangyuan
的一、二阶往复惯性力,这里假定曲轴为三曲拐。其中一级往复质量ms1为1.8kg,二级往复质量ms2也为1.8kg,曲柄半径为0.0375m,曲柄半径连杆比λ为37.5/195,角速度ω为2π×(800/60)rad/s,现将上述结构参数分别代入上文中所列的相关公式中,运用计算机内EXCEL程序列表、绘图计算分析,其结果如下:
1)按图1形式作顺时针转动,其一、二阶惯性力矢端力图如图1所示。
计算结果表明:当按照图1所示建立的直角坐标系xoy后,按照顺时针转θ角后,一阶往复惯性力如IⅠ(θ)所示,它是一个圆;二阶往复惯性力如IⅡ(θ)所示,它是一个很明显的椭圆。一阶惯性力的半径长为711N,图中显示了当θ=0°,一阶惯性力的向量是IⅠ(0),在这个位置曲柄矢与一阶惯性力矢瞬时重合,随后二者的方向矢量始终是关于竖直轴对称。二阶惯性力图是一个标准的椭圆,二阶惯性力的长半轴、短半轴为136.7N、45.6N,长轴始终在水平方向,长短轴之比为3:1。图中还显示了当θ=0°,二阶惯性力的向量是IⅡ(0)。由于这种对称布置,初始的二阶惯性力向量与曲柄矢重合,当曲轴旋转一周时,二阶惯性力是从IⅡ(0)位置开始沿着其二阶力椭圆形式反时针转动了2周,而一阶力则沿着外面的椭圆反时针转动了1周。
2)按图2形式作反时针转动,其一、二阶惯性力矢端力图如图2所示。
这里需说明的是,一阶惯性力图还是图1中的那个大椭圆,方向矢则逆着曲柄矢沿轨迹图顺时针变化。两矢量是关于竖直轴镜像对称。二阶惯性力图也类似这样,并且图2与图3起始的二阶惯性力矢量IⅡ(0)不变。
3)按图3形式作顺时针转动,其一、二阶惯性力矢端力图如图3所示。
应注意到对于往复质量固定的这些分布的型式,一、二阶惯性力矢图非常相似。也就是说,结构决定了力矢图。文末再提及一下二阶惯性力的椭圆应设法平衡,特别是在机器往大的方向发展时,往复质量ms、C值都变大时尤为需要。
注:本文未完待续,更多精彩内容见下期!
参考文献
(1)陆鹏程,复数法分析研究W型nianxiangyuan
往复惯性力(一~四)[J],nianxiangyuan
,2024.8~11期
(2)宋瑞林,气缸夹角为60°的V6车用发动机往复惯性力的平衡分析,[J],汽车技术,1988.8
(3)李松虎,3W型活塞nianxiangyuan
往复惯性力的分析,[J],nianxiangyuan
技术,1987.3
(4)陆鹏程,张光胜,三星型nianxiangyuan
振动问题研究,[J],安徽工程科技学院学报,2009.1
(5)王再顺,夹角为90°的V型nianxiangyuan
往复惯性力平衡的探讨,[J],nianxiangyuan
技术,1986.2
作者简介
陆鹏程,男,安徽桐城人,海军工程大学在职硕士毕业。现在中国人民解放军第四八一二工厂,安徽华晶机械有限公司工作,高级工程师。研究方向:nianxiangyuan
研究与强度设计。
【乐虎集团的官方网站 】一、序言
W型nianxiangyuan 在工业应用上非常常见,然而它内部的结构绝大多数都是单曲拐结构。能不能将曲轴设计成三曲拐的结构?
记得十多年前在新闻联播中看过沈鼓、陕鼓一些大型nianxiangyuan 三曲拐曲轴加工的画面,当时就想过小型W型无油机能否也采用这种三曲拐的结构?现在的一些nianxiangyuan 教材里没有提及角度式三曲拐W型nianxiangyuan ,仅是详细分析介绍了角度式单曲拐W型60°nianxiangyuan 一些理论。三曲拐的曲轴在一些大型的卧式机器中有应用,课本中对这种结构的机器进行了惯性力的分析。虽然目前教材上没有提及该种结构,但不代表这种结构不能合法存在。只是这种结构在一阶惯性力平衡方面有它的弊端,然而在其它方面也有它的优点。因前期对单曲拐W型各种角度的nianxiangyuan 一、二阶往复惯性力进行了详细分析计算,因而信手拈来将三曲拐的结构也进行详细分析,期望从理论上揭示该种结构的特点,以期扩展nianxiangyuan 的结构,推动国内nianxiangyuan 技术的发展。
本文以关于中心点对称的三曲拐、W型各种角度式nianxiangyuan 为例,考虑到往复质量的差异,从理论上分析推导出机器的一、二阶往复惯性力的公式,分析各种因素对机器的影响,从而遴选出性价比高的结构,可以尝试作为未来的工业应用。该惯性力作用点为曲轴箱体中心点,其大小和变化形成了惯性力的矢端轨迹力图。根据该公式,提出合适的平衡一、二阶往复惯性力的措施。创新拓展nianxiangyuan 理论和结构型式,推动全球范围内W型nianxiangyuan 的升级换代。
二、基础理论
1.正方向的问题
三曲拐W型nianxiangyuan 是指曲轴有三个拐,拐拐之间互成120°且不在同一个运动平面,能够获得旋转惯性力的自动平衡。三个拐所装配的连杆中心距相等,如图1所示。我们这里考虑两级nianxiangyuan ,它有两个一级一个二级,设一级的往复部件质量为ms1,二级往复部件质量为ms2,以图1中间的一列ms2为基准建立直角坐标系xoy,图2与图3中都是以ms2列为基准建立坐标系,这是考虑到有两种质量参与计算的方便。然而对于ms2列偏置分布建立的坐标系不是系统结构的主方向,不容易看出一、二阶惯性力的特征,需要运用到坐标矩阵变换关系式。规定投影到曲柄方向为x轴,与曲柄垂直的方向为y轴。这里规定x轴正方向是由机器中心向外指,这与nianxiangyuan 中将连杆受拉伸规定为正值相吻合,nianxiangyuan 动力计算时也将曲柄在上死点位置时运动部件受到的往复惯性力为正的最大值。y轴的正方向规定为将x轴顺旋转方向转一直角方向为其正方向。这样的规定都是为了方便计算,为后面的各种计算打下基础,也更容易发现规律。
2.研究手段问题
本文采用欧拉公式研究三列惯性力矢量的合力问题,将教科书上推导过程中采用垂直和水平方向两个式子合并成一个式子,这里规定x轴代表向量的实部,y轴代表向量的虚部,二者连接采用虚数单位i来连接。运用到的相关公式如下:

e为工程指数,i为虚数单位,θ为曲柄转角,单位为弧度,规定顺时针旋转方向为正值,θ为变量函数。该式子描述的也就是单位圆。

该式子也是上复数的共轭复数。

一阶惯性力是余弦函数,本文将一对互为共轭的复数的平均值来研究一、二阶惯性力。

它巧妙地运用到两个不同相位的欧拉函数的代数和来研究惯性力的投影问题。式子的右边正好是图1中右边列一阶惯性力投影到xoy坐标系上两个方向上两个力的大小。图1中气缸间夹角γ为60°,由于曲拐间的夹角都是120°,所以右边的活塞工作相位值为![]() ,根据前面规定了x、y轴的正方向,注意到上式的虚部应为正值。上式子描述的力是相对于中间为基准超前的列的一阶惯性力。大家发现,该式子就是将单曲拐落后的列的力的代数式取其共轭复数来计算。
,根据前面规定了x、y轴的正方向,注意到上式的虚部应为正值。上式子描述的力是相对于中间为基准超前的列的一阶惯性力。大家发现,该式子就是将单曲拐落后的列的力的代数式取其共轭复数来计算。
将该式的“γ”用“-γ”代替后形成新的公式就是图1中左边列的一阶惯性力。




该式子是图1中左边列二阶惯性力投影到xoy坐标系上两个方向上两个力的大小。可以验算当θ为0时,该列的相位角为-60°,所以其二阶惯性力为上式。同样的,将该式的“γ”用“-γ”代替后形成新的公式就是图1中右边列的二阶惯性力的计算公式。
上面两个公式仅对夹角为60°的适用,对其它角度例如45°的要给予修正。
3.研究切入点问题
本文研究惯性力的计算公式及其图像,顾及三列不同的往复质量对计算公式的影响,所以研究的起始点非常重要。文章分析了两种往复质量的计算公式,为计算方便,通常θ角的计入零点规定为ms2列活塞处于上死点的位置。文中得到的计算公式与选择上面的计入零点无关,也就是说,当将自变量θ转换成主方向位置时,只需要将所有公式里作相应的带入变换。
三、计算过程
文中分析了ms2列活塞居中布置和偏置一边时顺时针及反时针旋转时一、二阶往复惯性力的计算公式。考虑到二级nianxiangyuan 有两种往复质量,居中布置与偏置布置结构上有所不同,需要针对各自的型式进行单独研究,得到的惯性力公式形式迥异,所进行的坐标系矩阵变换工作量也不相同,偏置布置需要进行大量的矩阵变换而居中布置无需进行;偏置布置时顺、反时针旋转这两种情况比较起来,得到的惯性力公式基本相同,仅相差几个正负号而已。
三列活塞套入三个曲柄销的先后顺序形成的惯性力矩也各不相同,虽然微小,本文不作研究。文中假设三列都在同一个往复运动平面上往复惯性力合成后的矢端轨迹图像。
1.用基础理论分析图1形式三曲拐顺时针转动时惯性力


r为曲柄半径。ω为旋转角速度,以弧度计入计算。C为后文列出的公式书写方便引入的记号。

1.1一阶惯性力的计算


上式若采用三角函数来运算,则就是下面的两个式子






对(7)式再进行运算化简

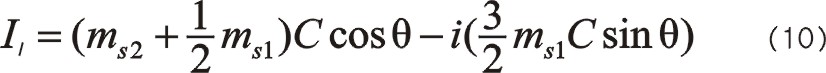
这是居中布置时三曲拐W型夹角60°一阶往复惯性力复数表达式。


当两个质量相等时,即是

一阶力矢在ms2=ms1时成圆的变化,其方向与曲柄转动的方向正好相反,大小与单曲拐的该种型式相同。不能采用在曲柄的反方向加一合适的平衡重来完全平衡掉一阶往复惯性力,需要采用其它合适的机构来平衡一阶惯性力。
若ms2>ms1,则此时的一阶惯性力图是椭圆。由于ms2居中分布时所建立的坐标系属于主方向的位置,其一阶惯性力运动形式与单曲拐的该种结构比较起来,惯性力图形状相同仅转动方向不同,所以它们的长轴都在x轴上,也就是图示中的竖直方向,短轴在水平方向。这种情形不同于偏置分布时的状况。
1.2二阶惯性力的计算


式中λ为曲柄半径连杆比。






这是居中布置时三曲拐W型夹角60°二阶往复惯性力复数表达式。





同样的,若采用三角函数来运算,则是下面的两个式子






二阶力矢在ms2=ms1时成短长轴比为1:3的椭圆变化。这种布置时θ为0°时,力矢到达该椭圆的短半轴位置,曲柄方向矢与二阶力矢在同一方向,但在该瞬时曲柄转向与二阶惯性力变化方向互为反方向。二阶惯性力旋转方向与单曲拐的该种型式不同。
若ms2>ms1,同样的,由于ms2居中分布时所建立的坐标系属于主方向的位置,其二阶惯性力运动形式与单曲拐的该种结构比较起来,惯性力图形状相同仅转动方向不同,所以这种情形时会使原短长轴比为1:3的椭圆有所微量变化。但不会引起椭圆偏转,这与偏置分布时的不同。一、二阶惯性力图因往复质量的不同都不会引起椭圆偏转可以理解为,左右两个ms1共同作用所引起的惯性力的合力导致的。
2.用基础理论分析图2形式三曲拐顺时针转动时惯性力

2.1一阶惯性力的计算





该式用到了三角函数的和差化积公式。




上式表明,一阶惯性力矢端轨迹是一椭圆,变化的周期和曲轴旋转的周期相同。在建立的xoy直角坐标系中,该椭圆的图像是标准的椭圆图像。如果从主方向即x'oy'直角坐标系来看,它不是标准椭圆,相当于将该主方向上的标准椭圆反时针旋转了30°。
若ms2>ms1,长半轴为 ,长轴在ms2列气缸轴线上;短半轴为
,长轴在ms2列气缸轴线上;短半轴为 ,短轴在ms1列气缸轴线上。由于ms2偏置分布时所建立的坐标系不属于主方向的位置,其一阶惯性力运动形式与单曲拐的该种结构比较起来,惯性力图形状相同仅转动方向不同。若ms2=ms1,椭圆退化成圆,半径为
,短轴在ms1列气缸轴线上。由于ms2偏置分布时所建立的坐标系不属于主方向的位置,其一阶惯性力运动形式与单曲拐的该种结构比较起来,惯性力图形状相同仅转动方向不同。若ms2=ms1,椭圆退化成圆,半径为 。
。
2.2二阶惯性力的计算









这是该种偏置布置不向自身旋转时三曲拐W型夹角60°二阶往复惯性力复数表达式。

这是其二阶惯性力参数方程的表达式。
为寻找上方程所描述的图像,先假定两个往复质量相等,利用寻找两个变量的二次多项式方程方法和矩阵转换法来进行。下面仿上面的假设,推导出它是一椭圆的依据。




根据线性代数中二次多项式的判别式定理,满足上两个条件,所以二阶惯性力也是一个椭圆。
由图1可以看出,原坐标系作正值旋转30°后到x'oy'坐标系,也就是将坐标系作逆时针旋转30°,作坐标系的矩阵变换的因子为



上式清晰地表明二阶惯性力的轨迹是椭圆,变化的周期是曲轴旋转周期的一半。经坐标系的旋转变换后的参数方程表明:该椭圆的长半轴是短半轴的3倍,二阶惯性力旋转方向与单曲柺的该种型式不同,曲柄转向与二阶惯性力变化方向互为反方向。不论是在xoy坐标系还是在x'oy'坐标系中,其椭圆的长半轴始终在水平方向,这与三列活塞在旋转平面的分布紧密联系。后文还分析表明,不论ms2处于偏置还是中间位置,不论旋转方向,二阶惯性力矢端力图始终是椭圆,该椭圆的长轴始终处于水平方向,不过其相位变化比较复杂。式(27)可以看出θ为15°时,力矢到达该椭圆的长半轴正的位置,这两个矢量不在同一方向成15°;θ为60°时,力矢到达该椭圆的短半轴负的位置,这两个矢量不在同一方向成120°。二阶惯性力的变化比曲轴自身旋转变化快一倍。
结合图2可得,形如式(25)、(26)参数方程,其图像是将标准直角坐标系中短长轴之比为1:3的椭圆反针旋转30°所得到的图象。
若ms2>ms1,同样的,由于ms2偏置分布时所建立的坐标系不属于主方向的位置,其二阶惯性力运动形式与单曲拐的该种结构比较起来,惯性力图形状相同仅转动方向不同,所以这种情形时会使原短长轴比为1:3的椭圆有所微量变化,并且会引起椭圆偏转。这是由于同一侧两个ms1共同作用所引起的惯性力的合力导致的。ms2列质量越大,原1:3的椭圆长轴越靠近ms2列,亦即长轴向ms2列旋转,这与单曲拐的一样仅二阶惯性力的旋转方向不同。
3.用基础理论分析图3形式三曲拐反时针转动时惯性力

3.1一阶惯性力的计算







该式表明反时针旋转时,一阶惯性力复数方程和直角坐标方程形式上与顺时针旋转时完全相同,说明同是三曲拐W型60°布置时,轨迹力图与转向无关,上述这种布置曲柄矢和一阶惯性力旋转矢也是互为反方向。当二者质量相等时,就成圆的变化,但不能在曲柄的反方向加一合适的平衡重来平衡一阶往复惯性力,需要设计其它的机构来平衡一阶惯性力。
在建立的xoy直角坐标系中,该椭圆的图像是标准的椭圆图像。如果从主方向即x'oy'直角坐标系来看,它不是标准椭圆,相当于将该主方向上的标准椭圆反时针旋转了30°。
3.2二阶惯性力的计算





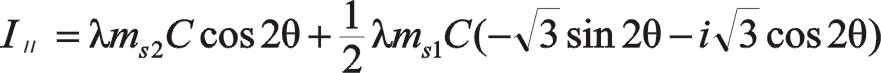


上式表明反时针旋转时,二阶惯性力直角坐标方程形式上与顺时针旋转时不同。说明换一个方向旋转时,需要另一种方程描述二阶惯性力的表现形式,后文的计算表明,它们的轨迹力图是相同的。文章从理论提供了这些状况时力矢的数学表达式,理论上也能够找到一种合适的机构加装上来平衡二阶往复惯性力。




坐标系作负值30°旋转变换到x'oy'坐标系中



结合图3可得,形如式(30)、(31)参数方程,其图像是将标准直角坐标系中短长轴之比为1:3的椭圆顺针旋转30°所得到的图象。
4.一致性验算
由图1、图2、图3,利用坐标系的旋转变换得出其公式的一致性。










也可以由向自身旋转时的代数方程推导出不向自身旋转时的代数方程,而不经过中间列来过渡,即由图3与图2之间的关系,将图3的状况依图示旋转120°后就是图2的状况。其矩阵方程如下





上式二阶方程验算过程的成立是通过下面的矩阵乘法运算得到的:

5.总结
从上面的三种情况分析和计算,可以得出三曲拐W型60°布置有两个ms1,一个ms2往复质量时有以下结论:
5.1一阶惯性力是一椭圆,ms2列中心线是该椭圆的一个对称轴方向,不论ms1、ms1、ms2在运动平面上如何分布,若ms2>ms1,则长轴在ms2列方向,反之则短轴在ms2列方向。
5.2二阶惯性力也是一椭圆,若ms1=ms2,不论采用上面三种情况的特殊情形来计算,该椭圆的长轴始终在水平方向,短轴在竖直方向,并且长半轴是短半轴的3倍。
5.3曲柄矢和一阶、二阶惯性力旋转矢都是互为反方向,这与单曲拐的完全不同而数值相同。
5.4以上讨论的都是关于惯性力对于往复质量ms以及夹角γ对其图像的影响,也讲到了实时的相位对应实时的图像。如果我们从惯性力图像变化率角度来刻画这一理论,就需要用到开普勒定律,这在论文总结中详细论述。
四.举例分析
本文以安徽华晶机械有限公司生产的WW-0.9/10B-Q型单曲拐全无油空压机为例分析该二级nianxiangyuan 的一、二阶往复惯性力,这里假定曲轴为三曲拐。其中一级往复质量ms1为1.8kg,二级往复质量ms2也为1.8kg,曲柄半径为0.0375m,曲柄半径连杆比λ为37.5/195,角速度ω为2π×(800/60)rad/s,现将上述结构参数分别代入上文中所列的相关公式中,运用计算机内EXCEL程序列表、绘图计算分析,其结果如下:
1)按图1形式作顺时针转动,其一、二阶惯性力矢端力图如图1所示。
计算结果表明:当按照图1所示建立的直角坐标系xoy后,按照顺时针转θ角后,一阶往复惯性力如IⅠ(θ)所示,它是一个圆;二阶往复惯性力如IⅡ(θ)所示,它是一个很明显的椭圆。一阶惯性力的半径长为711N,图中显示了当θ=0°,一阶惯性力的向量是IⅠ(0),在这个位置曲柄矢与一阶惯性力矢瞬时重合,随后二者的方向矢量始终是关于竖直轴对称。二阶惯性力图是一个标准的椭圆,二阶惯性力的长半轴、短半轴为136.7N、45.6N,长轴始终在水平方向,长短轴之比为3:1。图中还显示了当θ=0°,二阶惯性力的向量是IⅡ(0)。由于这种对称布置,初始的二阶惯性力向量与曲柄矢重合,当曲轴旋转一周时,二阶惯性力是从IⅡ(0)位置开始沿着其二阶力椭圆形式反时针转动了2周,而一阶力则沿着外面的椭圆反时针转动了1周。
2)按图2形式作反时针转动,其一、二阶惯性力矢端力图如图2所示。
这里需说明的是,一阶惯性力图还是图1中的那个大椭圆,方向矢则逆着曲柄矢沿轨迹图顺时针变化。两矢量是关于竖直轴镜像对称。二阶惯性力图也类似这样,并且图2与图3起始的二阶惯性力矢量IⅡ(0)不变。
3)按图3形式作顺时针转动,其一、二阶惯性力矢端力图如图3所示。
应注意到对于往复质量固定的这些分布的型式,一、二阶惯性力矢图非常相似。也就是说,结构决定了力矢图。文末再提及一下二阶惯性力的椭圆应设法平衡,特别是在机器往大的方向发展时,往复质量ms、C值都变大时尤为需要。
注:本文未完待续,更多精彩内容见下期!
参考文献
(1)陆鹏程,复数法分析研究W型nianxiangyuan 往复惯性力(一~四)[J],nianxiangyuan ,2024.8~11期
(2)宋瑞林,气缸夹角为60°的V6车用发动机往复惯性力的平衡分析,[J],汽车技术,1988.8
(3)李松虎,3W型活塞nianxiangyuan 往复惯性力的分析,[J],nianxiangyuan 技术,1987.3
(4)陆鹏程,张光胜,三星型nianxiangyuan 振动问题研究,[J],安徽工程科技学院学报,2009.1
(5)王再顺,夹角为90°的V型nianxiangyuan 往复惯性力平衡的探讨,[J],nianxiangyuan 技术,1986.2
作者简介
陆鹏程,男,安徽桐城人,海军工程大学在职硕士毕业。现在中国人民解放军第四八一二工厂,安徽华晶机械有限公司工作,高级工程师。研究方向:nianxiangyuan 研究与强度设计。





网友评论
条评论
最新评论